kaldi学习笔记（五）特征提取

原理

语音识别的第一步就是特征提取了，本文主要讲述如何根据音频信号提取MFCC和FBank特征（还有PLP，做孤立词识别用过，但没深究），这两种特征也是目前语音识别中使用最广泛的特征了。目前还有wav2vec也可以做特征提取，在无监督语音识别效果不错。

语音产生的过程：肺部呼出气体，然后通过声门的开启与闭合产生的周期信号，再通过声道产生声音，因为声道的不同，产生的声音也不同，比如拼音a、o、zi，三个声韵母，你会发现你的口型和牙齿的变化是不同的（可以看看台大李琳山老师的课）。而人类的语音信号大部分是在10000Hz以下，我们常使用的麦克风进行音频录制的采样率为16000Hz，一个采样点使用16bit来存储。

MFCC特征提取步骤

1.预加重

将语音信号通过一个预加重函数：

$$H(Z)=1-\mu z^{-1}$$,式中u的值介于0.9-1.0之间，通常取0.97。预加重的目的是提升高频部分，使信号的频谱变得平坦，保持在低频到高频的整个频带中，能用同样的信噪比求频谱。这是因为很多声音在高频的地方会变得很微弱，通过这个方法，这只是实验性的方法，因为worker，所有大家都用。

2.分帧

语音信号是一个非稳态、时变的信号，但是在极短的时间范围内，我们可以把语音认为是一个稳态、时不变的信号。这个极短时间范围通常分为20-40ms的帧，一般分成25ms为一帧。为了保证帧与帧之间平滑过渡，保持其连续性，分帧一般会让相邻的帧有重叠部分，因此每次只会移动10ms(而不是25ms)，这10ms我们称之为帧移。对于语音信号的采样频率是16kHz的，那么一帧就有16000*25/1000=400个样本点，帧移有16000 * 0.01 = 160 个样本点，如果最后一帧不够400个样本点，我们一般在后面补0。对于一段语音如果有n个点，可以得到(n-400)/160+1帧数据。

3.加窗

首先一个基础：时域的乘积等于频域的卷积

因为后面要做FFT，我们不可能对所有时间做FFT，只能对短时长度的信号做FFT，因此我们只能在整段语音上截取一小段进行FFT。我们人为已经对这个无限长序列加了一个矩形窗，也就是这个无限长序列的频谱已经和一个矩形窗函数的频谱做了卷积了。这时候卷积可不是相乘，自然输出的这个有限长序列输出的频谱就变形了。

我们对一段信号进行分帧处理的时候，频谱泄漏会影响分析，所以才会用到窗函数，而经过窗函数处理的时域信号，其初始点和结束点的时域振幅都接近0。

在语音识别上主要用的是”汉明窗“。它能使信号在窗边界的值近似为 0，从而使得信号趋近于是一个周期信号，一个完整的有限长周期函数可以代表一个无限长周期函数，因此周期函数不会造成频谱泄露，该窗函数如下：$$w[n]=0.54-0.46cos(\frac{2\pi n}{L}); 0\leq n \leq L-1$$，其他情况等于0。

注意：以下为对每一个窗口进行的操作

4.离散傅里叶变换

DFT,将每个窗口内的数据从时域信号转为频域信号。DFT 的变换公式如下：

$$X(m)=\sum_{n=0}^{N-1}{x(n)h(n)e^{-j2\pi nm/N}}$$

x(n) 是窗口中每个数据点的值，h(n)是一个数据点的窗函数，m是DFT的长度，e 是自然底数。有了X[m]我们就能估计功率谱：$$P_i(k)=\frac{1}{N}|X_i(m)|^2$$

上式得到的是周期图的功率谱估计。通常我们会进行512点的DFT,并且因为对称性只保留前257（第一个点是直流分量）个系数。在实际中使用的一般是快速傅里叶变换（FFT，大家可以自行了解）。

5.梅尔滤波器组

这个办法就是想要学人的耳朵怎么听语音的，研究人员发现听觉神经单元听到的是一堆频率而不是一个频率，而听觉神经是会听的重叠的，还有一个问题就是人耳对不同频率语音有不同的感知能力：对低频部分，与频率成线性关系；对高频部分，频率间隔越变越大。

因此研究人员想的一个办法就是用三角形滤波器来代替人耳神经单元，类似如下图所示：

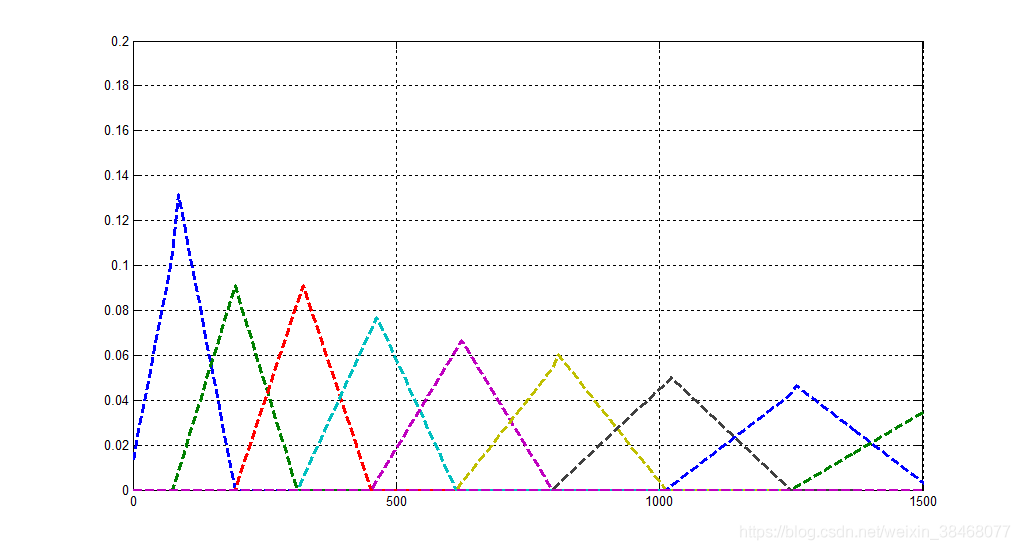
这是一组大约20-40（通常26）个三角滤波器组，它会对上一步得到的周期图的功率谱估计进行滤波，每个滤波器组由26个(滤波器)长度为257的向量组成，每个滤波器的257个值中大部分都是0，只有对于需要采集的频率范围才是非零。输入的257点的信号会通过26个滤波器，我们会计算通过每个滤波器的信号的能量。

对于重叠部分的问题，解决办法是将两个三角形按上图所示叠放在一起，上一个滤波器的中间频率作为下一个滤波器的开始频率。

对于不同频率感知不同，就是将频率Hz转换成Mel频率来解决，转换公式如下：

$$m=2595log_{10}(1+\frac{f}{700})$$

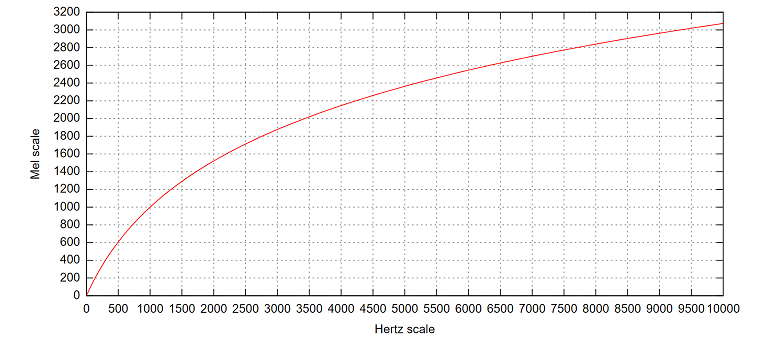
上图为Hz频率到Mel频率的转换。因此越到后面一个Mel滤波器对应的Hz频率越大，特性就是低频密，高频疏。

6.能量取log

字面意思，如果是40个滤波器，就对40个能量取log。也就得到了40维的Fbank特征。

为什么要取log:将在下一节介绍。

7.IDFT

FBank 特征的频谱图大概长下面这个样子，图中四个红点表示的是共振峰，是频谱图的主要频率，在语音识别中，根据共振峰来区分不同的音素（phone），所以我们可以把图中红线表示的特征提取出来就行，移除蓝色的影响部分。其中红色平滑曲线将各个共振峰连接起来，这条红线，称为谱包络（Spectral Envelope），蓝色上下震荡比较多的线条称为谱细节（Spectral details）。

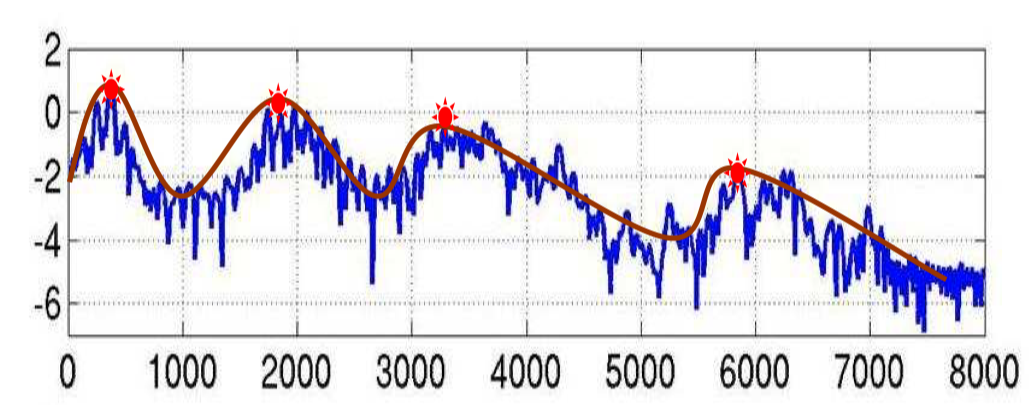
首先，开头我们就讲了语音的产生可以理解为呼出的气通过声带振动E(w)，然后经过腔体（包括舌头、牙齿等等）H(w)，形成各种不同的发音X(w)。其中声带产生的频谱E(w)是很简单的，主要就是腔体决定着各个音素的频谱。所以如果我们知道腔体的信息，就可以准确的对音素进行描述。显然的，腔体的形状对应着上面图中的谱包络(红色的线)，揭示了共振峰的走向。

现在我们希望获得这个红色的线，但是这个红色的线被蓝色的线干扰的很厉害，我们要怎么把蓝色的线除掉，要怎么去掉呢：

在时间轴上我们的语音可以看作：$$X[w]=E[w]*H[w]$$

将原来的语音经过傅里叶变换得到的频谱：$$X[w]=E[w]H[w]$$

因为phase信息对语音识别来说没用，因此只考虑幅度就是：$$|X[w]|=|E[w]||H[w]|$$

两边取log：$$log|X[w]|=log|E[w]|+log|H[w]|$$

再在两边取逆傅里叶变换得到：$$X[w]=E[w]+H[w]$$

log运算是为了分别包络和细节，包络代表音色，细节代表音高，显然语音识别就是为了识别音色。另外，人的感知与频率的对数成正比，正好使用log模拟，这就是取log的原因。

尽管现在E[w]+H[w]也就是包络和细节还是混在一起的，但是现在有一点不同，因为包络变化很慢，而细节变化很快，因此包络几乎在前面，而细节几乎再后面，所以我们如果在一个地方切开它，几乎就可以得到包络了，如下图所示。

一般来说IDFT用的是DCT(离散余弦变换)，因为DCT具有去相关性，这时我们得到40维倒谱系数，最后我们保留2-13这个12维，这12维就叫MFCC特征。对功率谱再做DCT的目的就是为了提取信号的包络。

8.Deltas和Delta-Deltas特征

Deltas和Delta-Deltas通常也叫(一阶)差分系数和二阶差分(加速度)系数。MFCC特征向量描述了一帧语音信号的功率谱的包络信息，但是语音识别也需要帧之间的动态变化信息，比如MFCC随时间的轨迹，实际证明把MFCC的轨迹变化加入后会提高识别的效果。因此我们可以用当前帧前后几帧的信息来计算Delta和Delta-Delta：

$$d_t=\frac{\sum_{n=1}^{N}{n(c_{t+n}-c_{t-n})}}{2\sum_{n=1}^{N}{n^2}}$$

上式得到的dt是Delta系数，计算第t帧的Delta需要t-N到t+N的系数，N通常是2。如果对Delta系数dt再使用上述公式就可以得到Delta-Delta系数，这样我们就可以得到3*12=36维的特征。上面也提到过，我们通常把能量也加到12维的特征里，对能量也可以计算一阶和二阶差分，这样最终可以得到39维的MFCC特征向量。

完成前面步骤后就是特征提取了，先看一下aishell脚本特征提取的代码

mfccdir=mfcc
for x in train dev test; do
  steps/make_mfcc_pitch.sh --cmd "$train_cmd" --nj 10 data/$x exp/make_mfcc/$x $mfccdir || exit 1;
  steps/compute_cmvn_stats.sh data/$x exp/make_mfcc/$x $mfccdir || exit 1;
  utils/fix_data_dir.sh data/$x || exit 1;
done

未完待续。。。